История возникновения понятия «Процент»

Три основные задачи на проценты

Задачи на расчет простого и сложного процента

Задачи на сплавы, растворы, смеси

Запись-схема для решения задач на проценты

В статье А.Е. Захаровой [9], мы узнали, что в финансовой практике для вычисления процентов чаще всего применяют такую форму записей, как схемы. Такой вид записи принято называть стандартной формой. Она имеет одно из преимуществ, что из неё сразу видно число процентов, на которое уменьшена или увеличена начальная сумма.

А.Е. Захарова предлагает рассмотреть наиболее типичные ситуации.

I. Если первоначальная цена некоторого товара составляла Sо денежных единиц, то после ее повы¬шения на р% она составит

Sо + Sо • р • 0,01 = Sо (1 + р • 0,01) (ден. ед.).

Аналогично, если первоначальная цена Sо по¬низилась на р%, то она составит

Sо (1 - р • 0,01) (ден. ед.).

Легко понять и запомнить эти формулы, если представить их в виде наглядных схем. Так, на рис. 1 повышение цены изображается стрелкой, идущей от Sо вверх, а понижение — стрелкой, направленной вниз от Sо .

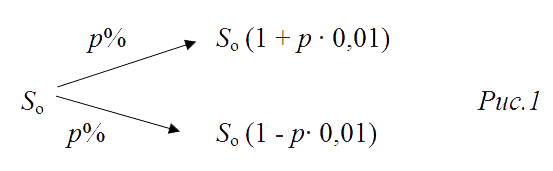
II. В результате повышения первоначальной цены Sо на р% и последующего понижения на q% окончательная цена равна

Sо (1 + p • 0,01)(1 - q •0,01) (ден. ед.).

Аналогично, если первоначальная цена Sо сна¬чала понизилась на p%, а потом повысилась на q%, то окончательная цена равна

Sо (1 - p • 0,01)(1 + q • 0,01) (ден. ед.).

Изображают такую схему в виде (рис. 2)

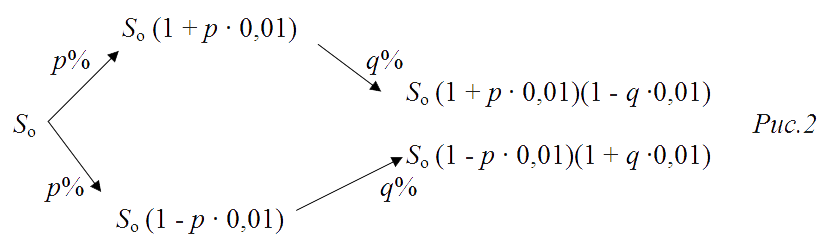
Перед тем как перейти к решению содержатель¬ных задач, выполним несколько задач подготовительного характера.

Задачи 1 2 3 4 5 6 Старинная задача

Задача1:До снижения цен книга в магазине стоила 120 рублей. Вычислите цену книги после двух последовательных снижений, если первое снижение было на 10%, а второе на 5%.

Решение:Пользуясь схемами, получаем: 120•(1-0,1)•(1-0,05) = 120•0,9•0,95= 108•0,95=102,6 (рубля) – цена книги после двух последовательных снижений.

Ответ: 102,6 рубля.

Задача 2:После снижения цен в магазине «Юнона» на 30% свитер стал стоить 2100 рублей. Сколько стоил свитер до снижения цен?

Воспользуемся схемами, получаем, что Sо •(1-30•0,01)=2100

Sо •0,7=2100;

Sо=3000

3000 (рублей) – стоил свитер до снижения цен.

Ответ: 3000 рублей.

Задача 3:Цена на молоко сначала снизилась на 5%, а затем повысилась на 5%. Изменилась ли первоначальная цена, и если да, то на сколько процентов?

Решение:Пусть исходная цена Sо , а окончательную за S, причем сначала составляют схему преобразований исход¬ной цены Sо (рис. 3) и только потом переходят к вычислениям:

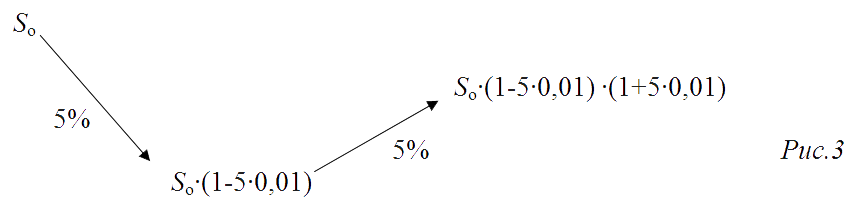
То есть: S= Sо•(1-5•0,01) •(1+5•0,01) = Sо•(1-25•0,0001)= Sо•(1-0,25•0,01)

Полученная стандартная форма записи показывает, что первоначальная цена понизилась на 0,25%.

Ответ: первоначальная цена понизилась на 0,25%.

Получив ответ на вопрос задачи, можно рассмотреть и такой вариант, изменится ли результат, если в задаче цена сначала повысится на 5%, а затем понизится на 5%. Вы¬вод такой, что результат изменения первоначальной цены не зависит от порядка произведенных преоб-разований и в этом случае первоначальная цена понизится на 0,25%.

Задача 4: (из данных сберегательного банка России) Вкладчик положил некоторую сумму на вклад «Молодежный» в сбербанк России. Через два года вклад достиг 2809 рублей. Каков был первоначальный вклад при 6% годовых?

Решение:Пусть х рублей первоначальный вклад.

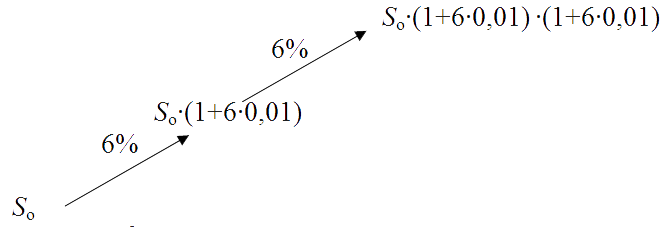
х•(1+0,06)²=2809

1,06²х=2809

1,1236х=2809

х=2500

Ответ: первоначальный вклад составлял 2500 рублей.

Задача 5: Цена мандарин в магазине поднялась на 25%, а потом еще на 30%. Груши поднялись в цене на 30% и стали по цене равной мандарин. Какова первоначальная цена мандарин, если груши до повышения цены стоили 125 рублей?

Решение:Обозначим искомую цену мандарин через х руб. Указанные в задаче преобразования цен можно изобразить на схеме (рис. 4) и составить уравнение, приравнивая новые цены на товары.

Уравнение х•(1 + 25 • 0,01) • (1 + 30 •0,01) = 125 • (1 + 30 • 0,01). Решая, находим, что х=100, то есть первона¬чальная цена мандарин 100 руб.

Ответ: 100 рублей.

Задача 6: (из рекламы) Сотовый телефон в «Евросети» стоил 3150 руб. После двух последовательных снижений цены он стал стоить 1512руб. Сколько стоил сотовый телефон после первого снижения, если второе снижение было на 20 процентных единиц больше, чем первое?

Решение: Пусть х процент первого снижения, тогда процент второго снижения - (х+20). Составим схему операций с первоначальной ценой товара.

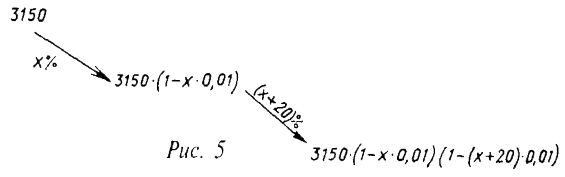
По условию окончательная цена телефона состав¬ляет 1512 руб., что служит основанием для состав¬ления уравнения:

3150 • (1 -х • 0,01) • (1 - (х + 20) • 0,01) = 1512.

Разделив обе части уравнения на 3150, получим (1 - 0,01х)(0,8 - 0,01х) = 0,48.

Вынесем из каждой скобки число 0,01:

0,01(100 - х) • 0,01(80 -х) = 0,48.

поделим обе части уравнения на 0,0001:

(100 -х)(80 -х) = 4800.

Итак, пришли к квадратному уравнению с целы¬ми коэффициентами

х²-180x+3200 = 0, корни которого вычисляются

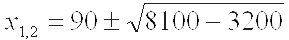
то есть

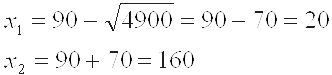
Итак,

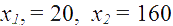
Второй корень не подходит по смыслу задачи (ина¬че продавец раздавал бы товар, приплачивая еще 60% его стоимости).

Найдем значение выражения 3150•(1-20•0,01)= 2520 (рублей).

Ответ: цена сотового телефона после первого снижения станет равной 2520рублей.

Старинная задача

Задача:М.В. Ломоносов тратил одну денежку на хлеб и квас. Когда цены выросли на 20%, на ту же денежку он приобрел полхлеба и квас. Хватит ли той же денежки хотя бы на квас, если цены ещё раз вырастут на 20%?

Решение:Пусть примем денежку за единицу, стоимость хлеба обозначим через х, а стоимость кваса – через у. Составим уравнения: до повышения цен х+у=1, а после повышения 1,2(0,5х+у)=1. Составим и решим систему уравнений:

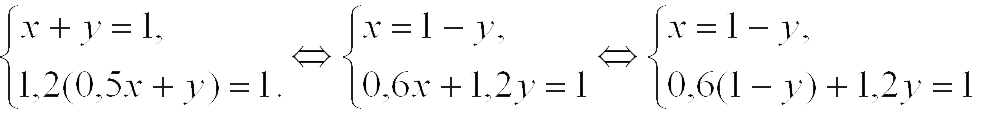
Решим второе уравнение 0,6(1-у)+1,2у=1, получаем, что у=2/3, а затем применяя схему

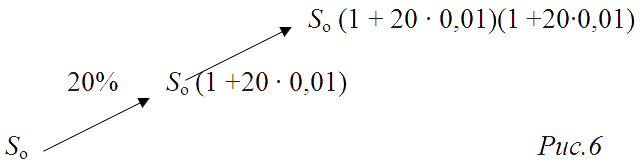
посчитаем 1,2•1,2у=1,2•1,2•2/3 = 0,96 - стоимость кваса после двух повышений цен.

Ответ: денежки хватит на квас.